16. Complex Numbers

Certain portions of these chapter require facts from other parts like determinants, equations etc. Student is encouraged to look ahead into these chapters for referenced results/equations used.

16.1. Imaginary Numbers

By definition a complex number has two components. A real part and an imaginary part. Now since we have not studied anything about imaginary numbers let us study them first. An imaginary number is a number which is imaginary. Err! What I mean is in practice you cannot have physical representation of those quantities. Square root of negative numbers are called imaginary numbers. For example,

\[\sqrt{-1}, \sqrt{-2}, \sqrt{-3}, ... \text{and so on} \]

We denote \(\sqrt{-1}\) with the Greek symbol \(i\), which stands for iota.

Clearly, we have the following:

\[i^2 = -1, i^3=-i, i^4=1\]

If you examine carefully you will find that following holds true:

\[i^{4m}=1,i^{4m+1} = i, i^{4m+2}=-1, \text{ and }i^{4m+3}=-i, \text{ where }m\in P\]

\(P\) is the set of positive numbers including zero. Proof of the above one is simple and therefore left as an exercise to reader.

Gotcha

Consider the following:

\[1 = \sqrt{1}=\sqrt{(-1)*(-1)}=\sqrt{-1}*\sqrt{-1}=i*i=-1\]

However, the above result is wrong. The reason being is that for any two real numbers \(a\) and \(b\) \(\sqrt{a}*\sqrt{b}=\sqrt{ab}\) holds good if and only if the two numbers are either zero or positive.

16.2. Problems

1. Evaluate:

   1. \(i^5\)

      \(i^5=i^2*i^2*i=-1*-1*i=i\)

   2. \(i^{67}\)

      \(i^{64}*i^2*i=-i\)

   3. \(i^{-49}\)

      \(\frac{1}{i^{48}i}=\frac{1}{i}=i^3\)

2. Prove that \(i^n+i^{n+1}+i^{n+2}+i^{n+3}=0\).

   \(i^n(1+i+i^2+i^3)=i^n(1+i-1-i)=0\)

16.3. Definitions Related to Complex Numbers

A typical complex number has two parts as stated above. It is commonly written as \(a+ib\) or \(x+iy\). Here, \(a, b, x\) or \(y\) all are real numbers. The complex number itself is denoted by \(z\). Therefore, we have \(z=x+iy\). Here, \(x\) is called the real part and is also denoted by \(Re(z)\) and \(y\) is called the imaginary part and is also denoted by \(Im(z)\).

A complex number is purely real if its imaginary part or \(y\) or \(Im(z)\) is zero. Similarly, a complex number is purely imaginary if its real part or \(x\) or \(Re(z)\) is zero. Clearly, as you can fathom that there can exist only one number which has both the parts as zero and certainly that is 0. That is, \(0=0+i0\).

The set of all complex number is typically denoted by \(C\). Two complex numbers \(z_1\) and \(z_2\) are said to be true if there real parts are equal and imaginary parts are equal. That is if \(z_1=x_1+iy_1\) and \(z_2=x_2+iy_2\) then \(x_1\) must be equal to \(x_2\) and similarly for imaginary part for two complex numbers to be equal.

16.4. Simple Operations

16.4.1. Addition

\((a+ib)+(c+id)=(a+c)+i(b+d)\)

16.4.2. Subtraction

\((a+ib)-(c+id)=(a-c)+i(b-d)\)

16.4.3. Multiplication

\((a+ib)*(c+id)=ac+ibc+iad+bdi^2=(ac-bd)+i(bc+ad)\)

16.4.4. Division

The complex number in denominator must not have both parts as zero. At least one part must be non-zero.

\[\frac{a+ib}{c+id}=\frac{(a+ib)(c-id)}{(c+id)(c-id)}=\frac{(ac+bd)+i(bc-ad)}{c^2+d^2}\]

16.5. Conjugate of a Complex Number

Let \(z=x+iy\) be a complex number then its complex conjugate is a number with imaginary part made negative and it is written as \(\bar{z}=x-iy\). \(\bar{z}\) is the typical representation for a conjugate of a complex number \(z\).

16.5.1. Properties of Conjugates

1. \(z_1=z_2\Leftrightarrow \bar{z_1}=\bar{z_2}\).

   Clearly as we know for two complex numbers to be equal both parts must be equal so this is very easy to understand that if \(x_1=x_2\) and \(y_1=y_2\) then this bidirectional condition is always satisfied.

2. \(\overline{(\bar{z})}=z\).

   \(z=x+iy\), hence, \(\bar{z}=x-iy\), hence, \(\overline{(\bar{z})}=x-(-iy)=x+iy=z\).

3. \(z+\bar{z}=2Re(z)\).

   Clearly, \(z+\bar{z}=x+iy+x-iy=2x=2Re(z)\).

4. \(z-\bar{z}=2iIm(z)\).

   Clearly, \(z-\bar{z}=x+iy-(x-iy)=2iy=2iIm(z)\).

5. \(z=\bar{z}\Leftrightarrow z\) is purely real.

   Clearly, \(x+iy=x-iy \implies 2iy=0 \implies y=0\). Therefore, \(z\) is purely real. Conversely if \(z\) is purely real then \(z=x\) therefore \(z=\bar{z}\).

6. \(z+\bar{z}=0\Leftrightarrow z\) is purely imaginary.

   It can be proven like previous point.

7. \(z\bar{z}=[Re(z)]^2+[Im(z)]^2\).

   Clearly, \(z\bar{z}=(x+iy)(x-iy)=(x^2+y^2)=[Re(z)]^2+[Im(z)]^2\).

8. \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\).

   Clearly, \(\overline{z_1+z_2}=\overline{(x_1+iy_1)+(x_2+iy_2)}\) i.e. \(\overline{(x_1+x_2)+i(y_1+y_2)}=(x_1+x_2)-i(y-1+y_2)\) i.e. \((x_1-iy_1)+(x_2-iy_2)=\overline{z_1}+\overline{z_2}\).

9. \(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\).

   It can be proven in the same fashion as 8 and left to the student.

10. \(\overline{z_1 z_2}=\overline{z_1}~\overline{z_2}\).

    It can be proven in the same fashion as 8 and left to the student.

\[\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}} \text{ if } z_2 \neq 0. \]

If you rationalize the base by multiplying it from its conjugate and apply division formula give above it can be easily proven hence left as an exercise.

12. If \(P(z)=a_0+a_1z+a_1z^2+...+a_nz^n\) where \(a_0, a_1,...,a_n\) and \(z\) are complex number, then

\[\overline{P(z)}=\overline{a_0}+\overline{a_1}~(\overline{z})+\overline{a_2}~(\overline{z})^2+ ... + \overline{a_n}~(\overline{z})^n=\overline{P}(\overline{z})\]

where

\[\bar{P}z=\overline{a_0}+\overline{a_1}~z+\overline{a_2}z^2+ ... + \overline{a_n}z^n \]

13. If \(R(z)=\frac{P(z)}{Q(z)}\) where P(a) and Q(z) are polynomials in z, and \(Q(z)\neq 0,\) then

\[\overline{R(z)}=\frac{\overline{P}(\overline{z})}{\overline{Q}(\overline{z})} \]

14. If

\[z = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{vmatrix}, \text{ then } \overline{z} = \begin{vmatrix} \overline{a_1} & \overline{a_2} & \overline{a_3} \\ \overline{b_1} & \overline{b_2} & \overline{b_3} \\ \overline{c_1} & \overline{c_2} & \overline{c_3} \\ \end{vmatrix} \]

where \(a_i, b_i, c_i (i=1, 2, 3)\) are complex numbers. To prove this you need to understand determinants.

16.6. Modulus of a Complex Number

Modulus of a complex number \(z\) is denoted by \(|z|\) and is equal to the real number \(\sqrt{x^2+y^2}\). Note that \(|z|\geq~0~\forall~z\in C\).

16.6.1. Properties of Modulus

1. \(|z|=0 \Leftrightarrow z=0\).

   Clearly, this means \(x^2+y^2=0 \implies x=0 \text{ and } y=0 \implies z=0\).

2. \(|z|=|\bar{z}|=|-z|=|-\bar{z}|\).

   Clearly, all result in to \(x^2+y^2\).

3. \(-|z|\leq Re(z)\leq |z|\).

   Clearly, \(-(x^2+y^2)\leq x^2\leq (x^2+y^2)\).

4. \(-|z|\leq Im(z)\leq |z|\).

   Clearly, \(-(x^2+y^2)\leq y^2\leq (x^2+y^2)\).

5. \(z\bar{z}=|z|^2\).

   Clearly, \((x+iy)(x-iy)=x^2+y^2=|z|^2\).

Following relations are very easy and can be proved by the student. If \(z_1\) and \(z_2\) are two complex numbers then,

6. \(|z_1 z_2|=|z_1||z_2|\).

   Clearly, \(|z_1 z_2|=|x_1x_2-y_1y_2+i(x_1y_2+x_2y_1)|\) i.e. \(\sqrt{(x_1x_2-y_1y_2)^2+(x_1y_2+x_2y_2)^2}\) i.e. \(\sqrt{(x_1+y_1)^2(x_2+y_2)^2}=|z_1||z_2|\).

7. \[\left|\frac{z_1}{z_2}\right|=\frac{|z_1|}{z_2}, \text{ if } z_2\neq 0. \]

8. \(|z_1+z_2|^2=|z_1|^2+|z_2|^2+\overline{z_1}z_2+z_1\overline{z_2}\) i.e. \(|z_1|^2+|z_2|^2+2Re(z_1\overline{z_2})\).

9. \(|z_1-z_2|^2=|z_1|^2+|z_2|^2-\overline{z_1}z_2-z_1\overline{z_2}\) i.e. \(|z_1|^2+|z_2|^2-2Re(z_1\overline{z_2})\).

10. \(|z_1+z_2|^2+|z_1-z_2|^2=2(|z_1|^2+|z_2|^2)\).

11. If \(a\) and \(b\) are real numbers and \(z_1\) and \(z_2\) are complex numbers, then

    \(|az_1+bz_2|^2+|bz_1-az_2|^2=(a^2+b^2)(|z_1|^2+|z_2|^2)\)

12. If \(z_1, z_2 \neq 0\), then \(|z1+z2|^2=|z_1|^2+|z_2|^2\Leftrightarrow \frac{z_1}{z_1}\) is purely imaginary.

13. If \(z_1\) and \(z_2\) are complex numbers then \(|z_1+z_2|\leq|z_1|+|z_2|.\) This inequality can be generalized also.

14. Similarly, these can also be proven that \(|z_1-z_2|\leq|z_1|+|z_2|,\) \(||z_1|-|z_2||\leq|z_1|+|z_2|\) and \(|z_1-z_2|\geq||z_1|-|z_2||.\)

16.7. Geometrical Representation

A complex number z which we have considered to be equal to x+iy in our previous representations can be represented by a point P whose Cartesian coordinates are (x,y) referred to rectangular axes Ox and Oy where O is origin i.e. (0, 0) and are called real and imaginary axes respectively. The xy two-dimensional plane is also called Argand plane, complex plane or Gaussian plane. The point P is also called the image of the complex number and z is also called the affix or complex coordinate of point P.

Now as you can easily figure out that all real numbers will lie on real axis and all imaginary numbers will lie on imaginary axis as their counterparts will be zero.

The modulus is given by the length of segment OP which is equal to \(OP=\sqrt{x^2+y^2} = |z|.\) This, \(|z|\) is the length of the OP. Given below is the graphical representation of the complex number.

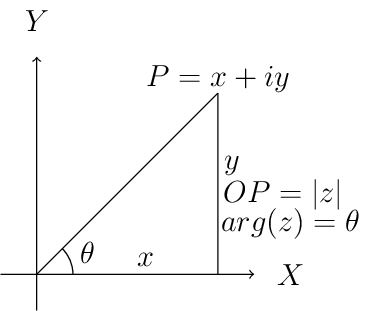
Complex number in argand plane or complex plane

In the above diagram \(\theta\) is known as the argument of z. This is nothing but angle made with positive direction (i.e. counter-clockwise) of real axis. Now this argument is not unique. If \(\theta\) is an argument of a complex number z then \(2n\pi+\theta\) where \(n\in I\) where I is the set of integers. The value of argument for which \(-\pi<\theta\leq\pi\) is called the principal value of argument or principal argument.

16.7.1. Different Arguments of a Complex Number

In the diagram given above the argument is given as

\[arg(z) = tan^{-1}\left(\frac{y}{x}\right) \]

this value is for when z is in first quadrant.

When z will lie in second, third and fourth quadrants then arguments will be

\[arg(z) = \pi - tan^{-1}\left(\frac{y}{|x|}\right) arg(z) = -\pi + tan^{-1}\left(\frac{|y|}{|x|}\right) arg(z) = -tan^{-1}\left(\frac{|y|}{x}\right)\]

respectively.

16.7.2. Polar Form of a Complex Number

If z is a non-zero complex number, then we can write \(z=r(cos\theta + isin\theta)\) where \(r=|z|\text{ and }\theta=arg(z).\)

In this case z is also given by \(z=r(cos(2n\pi+\theta)+i~sin(2n\pi+\theta))\) where \(n\in I.\)

16.7.2.1. Euler’s Formula

The complex number \(cos\theta+i~sin\theta\) is denoted by \(e^{i\theta}\) or \(c\) is \(\theta.\)

16.7.3. Important Results Involving Arguments

If \(z, z_1 \text{ and } z_2\) are complex numbers then

1. \(arg(\overline{(z)}) = arg(z)\). This can be easily proven as if \(z=x+iy\) then \(\overline{z}=x-iy\) i.e. sign of argument will get a -ve sign as y gets one.

2. \(arg(z_1z_2)=arg(z-1)+arg(z_1)+2n\pi\) where

\[k = \begin{cases} 0 \text{ if } & -\pi

3. Similarly, \(arg(z_1, \overline{z_2})=arg(z_1)-arg(z_2)\)

4. \(arg\left(\frac{z_1}{z_2}\right)=arg(z_1)+arg(z_2)+2n\pi\)

5. \(|z_1+z_2|=|z_1-z_2|\Leftrightarrow arg(z_1)-arg(z_2)=\pi/2\)

6. \(|z_1+z_2|=|z_1|+|z_2|\Leftrightarrow arg(z_1)=arg(z_2)\)

7. \(|z_1+z_2|^2 = r_1^2+r_2^2+2r_1r_2cos(\theta_1-\theta_2)\)

8. \(|z_1-z_2|^2 = r_1^2+r_2^2+2r_1r_2cos(\theta_1+\theta_2)\)

16.8. Vector Representation

Complex numbers can also be represented as vectors. Length of the vector is nothing but modulus of complex number and argument is the angle which the vector makes with read axis. It is denoted as \(\overrightarrow{OP}\) where \(OP\) represents the vector of the complex number z.

16.9. Algebraic Operation’s Representation

Let \(z_1=x_1+iy_1\) and \(x_2+iy_2\) be two complex numbers which are represented by two points \(P1\) and \(P2\) in the following diagrams.

16.9.1. Addition

Now as we know that \(z_1+z_2 = (x_1+x_2)+i(y_1+y-2).\) Let us try to achieve this through geometrical means.

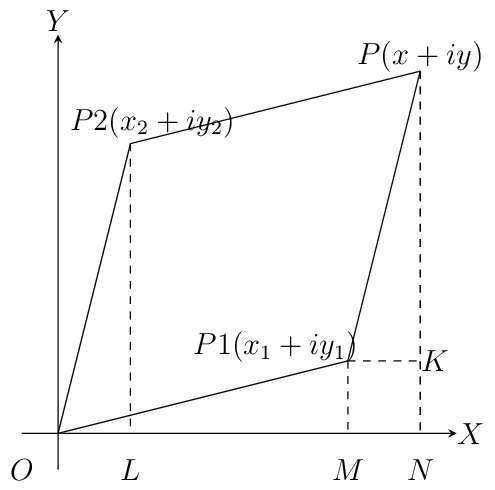
Complex number addition

Let us have \(P_2L, P_1M \text{ and } P_N\) perpendiculars from \(P_2, P_1 \text{ and } P\) respectively on x axis. Draw \(P_1K\) perpendicular to \(PN\). Note that triangles \(OP_2L\) and \(P_1P_2K\) are congruent. Very simple analysis will result in the fact that

\[OP=OP_1+OP_2 \]

16.9.2. Subtraction

TO subtract we will have to make \(P_2\) rotate by \(180^\circ .\) Now this means that in precious diagram it will fall in third quadrant and then again it can be proven that

\[z_1-z_2 = P_2P_1 \]

Similarly diagrams for multiplication and division can also be obtained and is left as an exercise.

For multiplication length or modulus of product is product of two modulii and argument is sum of arguments. For division modulus is division and argument is subtraction of two arguments. This implies

\[z_1z_2=r_1r_2(cos(\theta_1+\theta_2)+isin(\theta_1+\theta_2)) \]

and

\[\frac{z_1}{z_2}=\frac{r_1}{r_2}(cos(\theta_1+\theta_2)-isin(\theta_1-\theta_2)) \]

16.9.3. Three Important Results

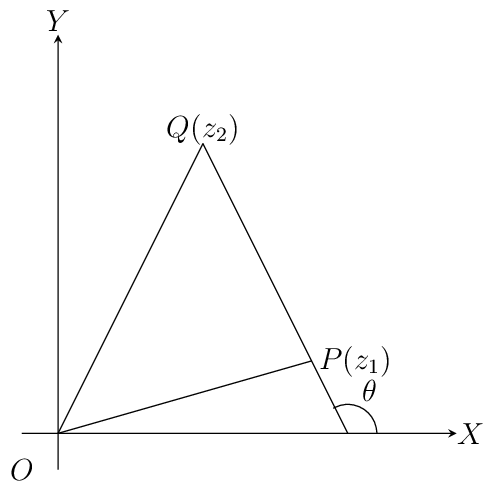
\(z_1-z_2=\overrightarrow{OP}-\overrightarrow{OQ}=\overrightarrow{QP}\)

\(\therefore |z_1-z_2|=|\overrightarrow{QP}|=QP,\) which is nothing but distance between points P and Q which are nothing but representation of complex numbers \(z_1\) and \(z_2.\)

\(arg(z_1-z_2)\) is the angle which \(\overrightarrow{QP}\) makes with positive direction of x-axis being denoted by \(\theta.\)

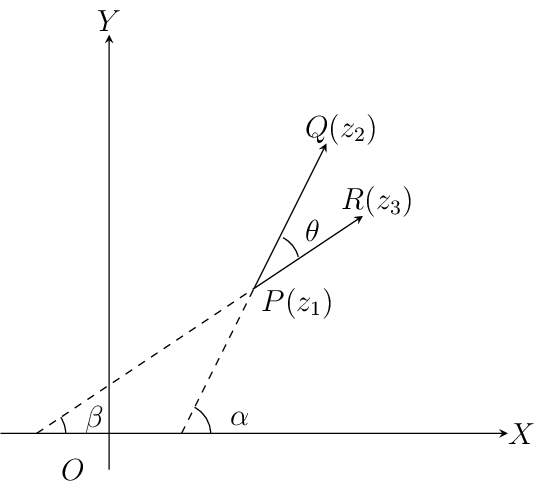
\(\theta=\alpha-\beta=arg(z_3-z_1)-arg(z_2-z_1)\)

\[\Rightarrow~\theta=arg\frac{z_3-z_1}{z_2-z_1} \]

Similarly if three complex numbers are vertices of a triangle then angles of those vertices can also be computed using previous results.

Similarly, for four points to be concyclic where those points are represented by \(z_1, z_2, z_3 \text{ and } z_4\) if

\[arg\left(\frac{z_2-z_4}{z_1-z_4}\frac{z_1-z_3}{z_2-z_3}\right)=0 \]

Note that these complex numbers are in either clockwise or counter-clockwise order as vertices of the quadrilateral.

16.10. More Roots

16.10.1. Any Root of an Imaginary Number is an Imaginary Number

Let \(x+iy\) be an imaginary number, where \(y\neq 0\)

Let \((x+iy)^n=a, \therefore x+iy = a^n\)

Now if \(a\) is real \(a^n\) will also be real but from above an imaginary number \(x+iy\) is equal to a real number \(a^n\) which is not possible. Hence, a must be imaginary.

16.10.2. Square Root of a Complex Number

Consider a complex number \(z=x+iy\) then let us say

\[\sqrt{x+iy}=a+ib x+iy = (a^2-b^2)+2abi\]

Equating real and imaginary parts

\[x=a^2-b^2 \text{ and } y=2ab \]

then we can write

\[a^2+b^2 = (a^2-b^2)^2 + (2ab)^2 \]

From two equations written above we have

\[a=\pm\sqrt{\left(\frac{\sqrt{x^2+y^2}+x}{2}\right)} \text{ and } b=\pm\sqrt{\left(\frac{\sqrt{x^2+y^2}-x}{2}\right)} \text{ and }\]

Thus, we can deduce our complex number.

16.10.3. Cube Roots of Unity

Let \(x=x^{\frac{1}{3}}\), then \(x^3-1=0.\)

\(\Rightarrow~(x-1)+(x^2+x+1)=0\)

So the three roots are \(x=1, x=\frac{-1\pm \sqrt{-3}}{2}\) i.e. \(1, \frac{-1+i\sqrt{3}}{2} \text{ and } \frac{-1-i\sqrt{3}}{2}.\)

It can be easily verified that if \(\omega=\frac{-1-i\sqrt{3}}{2}\) then \(\omega^2=\frac{-1+i\sqrt{3}}{2}\) thus three cube roots are represented as \(1, \omega \text{ and } \omega^2.\)

Similarly one of the properties is that \(1+\omega+\omega^2=0\) which can be verified also and product of all three is 1 i.e. \(\omega^3=1.\)

16.10.4. nth Root of Unity

\[1=cos0+isin0 \]

\[=1^\frac{1}{n}=(cos0+isin0)^\frac{1}{n} \]

\[=cos\frac{2k\pi+0}{n}+isin\frac{2k\pi+0}{n}, \text{ where } k=0,1,2,3,4,....(n-1)\]

\[=e^{\frac{i2k\pi}{n}} \]

\[= 1, e^\frac{i2\pi}{n}, e^\frac{i4\pi}{n}, ..., e^\frac{i2(n-1)\pi}{n} \]

\[= 1,\alpha , \alpha^2, ..., \alpha^n, \text{ where } \alpha=e^\frac{i2\pi}{n} \]

Similarly as cube roots of unity it can be proven that

\[1+\alpha+\alpha^2 + \alpha^{n-1}= 0 \]

and

\[1.\alpha.\alpha^2. ... .\alpha^{n-1}=(-1)^{n-1} \]

16.11. De Moivre’s Therorem

Statement: If \(n\) is any integer then \((cos\theta + isin\theta)^n=cosn\theta + isinn\theta\).

If \(n\) is any rational number then one of the values of \((cos\theta + isin\theta)^n=cosn\theta + isinn\theta\)

Proof:

Case I: When n is 0.

Clearly, \((cos\theta+isin\theta)^0=1\)

Case II: When n is a positive integer.

Clearly, \((cos\theta+isin\theta)^2=(cos^2\theta-sin^2\theta+i2cos\theta sin\theta)\)

= \(cos2\theta+isin2\theta\)

Similarly, \((cos\theta+isin\theta)^3=cos3\theta+isin3\theta\)

Similalrly, if for \(n-1\) we have

\((cos\theta+isin\theta)^{(n-1)} = cos(n-1)\theta+isin(n-1)\theta\) then it can be easily proven that

\((cos\theta+isin\theta)^n = cosn\theta+isinn\theta\)

It is left as an exercise to the reader to prove it for negative and fractional powers.

16.12. Some Important Geometrical Results and Equations

16.12.1. Section Formula

Let \(z_1=x_1+iy_1, z_2=x_2+iy_2\) then if \(z=z+iy\) which divides the previous two points in the ratio \(m;n\) can be given by using the results from coordinate geometry as below:

\[x=\frac{mx_2+nx_1}{m+n}, \text{ and } y=\frac{my_2+ny_1}{m+n} \therefore~z=\frac{mz_2+nz_1}{m+n}\]

Extending this section formula we can say that if there is a point which divides this line in two equal parts i.e. the point is mid-point then \(m = 1\) and \(n = 1\) then \(z\) is given by \(\frac{1}{2}(z_1 + z_2)\)

16.12.2. Distance Formula

Distance between \(A(z_1)\) and \(B(z_2)\) is given by \(AB = |z_1 - z_2|\)

16.12.3. Equation of a Line Passing Through Two Points

The equation between two point \(z_1\) and \(z_2\) is given by the determinant

\[\begin{vmatrix} z & \overline{z}&1\\ z_1 & \overline{z_1}&1\\ z_2 & \overline{z_2}&1 \end{vmatrix}=0 \]

or,

\[\frac{z-z_1}{\overline{z}-\overline{z_1}}=\frac{z_1-z_2}{\overline{z_1}-\overline{z_2}} \]

Please refer to determinants section and coordinate geometry books on how to establish this result.

The proof is left as an exercise to the reader.

The parametric form is given by \(z = iz_1 + (1 - t)z_2\)

16.12.4. Collinear Points

Three points \(z_1, z_2 \text{ and } z_3\) are collinear if and only if

\[\begin{vmatrix} z_1 & \overline{z_1}&1\\ z_2 & \overline{z_2}&1\\ z_3 & \overline{z_3}&1 \end{vmatrix}=0 \]

This follows from the formula for a line passing through two points. Just substitute \(z_3\) as a point in the equation to satisfy the equality.

16.12.5. Parallelogram

Four complex numbers \(A(z_1), B(z_2), C(z_3)\) and \(D(z_4)\) represent the vertices of a parallelogram if \(z_1 + z_3 = z_2 + z_4.\)

The diagonals \(AC\) and \(BD\) must bisect each other. Therefore,

\[\frac{1}{2}(z_1 + z_3) = \frac{1}{2}(z_2 + z_4) \Leftrightarrow z_1 + z_3 = z_2 + z_4\]

16.12.6. Rhombus

Four complex numbers \(A(z_1), B(z_2), C(z_3)\) and \(D(z_4)\) represent the vertices of a rhombus if \(z_1 + z_3 = z_2 + z_4\) and \(|z_4 - z_1| = |z_2 - z_1|.\)

The diagonals \(AC\) and \(BD\) must bisect each other. Therefore,

\[\frac{1}{2}(z_1 + z_3) = \frac{1}{2}(z_2 + z_4) \Leftrightarrow z_1 + z_3 = z_2 + z_4\]

Also, a pair of two adjacent sides are equal for example \(AD = AB\) thus second condition is also met i.e. \(|z_4 - z_1| = |z_2 - z_1\).

16.12.7. Square

Four complex numbers \(A(z_1), B(z_2), C(z_3)\) and \(D(z_4)\) represent the vertices of a square if \(z_1 + z_3 = z_2 + z_4, |z_4 - z_1| = |z_2 - z_1|\) and \(|z_3 - z_1| = |z_4 - z_2|.\)

The diagonals \(AC\) and \(BD\) must bisect each other. Therefore,

\[\frac{1}{2}(z_1 + z_3) = \frac{1}{2}(z_2 + z_4) \Leftrightarrow z_1 + z_3 = z_2 + z_4 \]

Also, a pair of two adjacent sides are equal for example \(AD = AB\) thus second condition is also met i.e. \(|z_4 - z_1| = |z_2 - z_1\).

And the two diagonals are equal i.e. \(AC = BD\) i.e. \(|z_3 - z_1| = |z_4 - z_2|.\)

16.12.8. Rectangle

Four complex numbers \(A(z_1), B(z_2), C(z_3)\) and \(D(z_4)\) represent the vertices of a rectangle if \(z_1 + z_3 = z_2 + z_4, |z_4 - z_1|\) and \(|z_3 - z_1| = |z_4 - z_2|.\)

Similar to above examples the diagonals bisect each other. Also, the diagonals \(AC\) and \(BD\) should be equal.

16.12.9. Centroid of a Triangle

Let \(A(z_1), B(z_2)\) and \(C(z_3)\) be the vertices of a \(\triangle ABC.\)

Centroid \(G(z)\) of the \(\triangle ABC\) is the point of concurrence of the medians of all three sides and is given by

\[z = \frac{1}{3}(z_1 + z_2 + z_3) \]

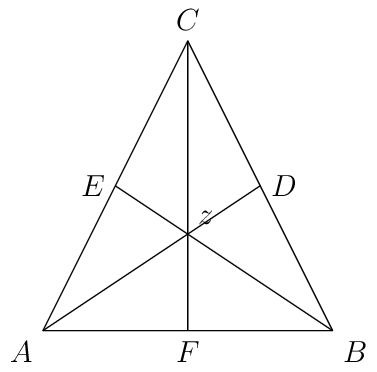
16.12.10. Incenter of a Triangle

Let \(A(z_1), B(z_2)\) and \(C(z_3)\) be the vertices of a \(\triangle ABC.\)

Incenter \(I(z)\) of the \(triangle ABC\) is the point of concurrence of internal bisectors of all the angles and is given by

\[z = \frac{az_1 + bz_2 + cz_3}{a + b + c} \]

where \(a, b\) and \(c\) are the lengths of the sides.

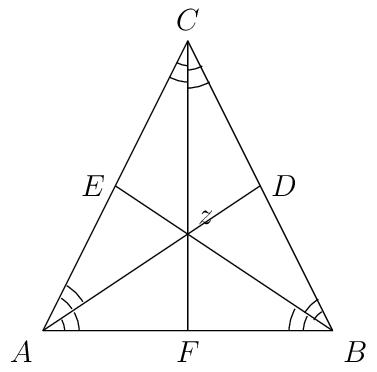
16.12.11. Circumcenter of a Triangle

The circumcenter \(S(z)\) of the \(\triangle ABC\) is the concurrence of perpendicular bisectors of sides of \(\triangle ABC\) and is given by

\[z = \frac{(z_2 - z_3)|z_1|^2 + (z_3 - z_1)|z_2|^2 + (z_1 - z_2)|z_3|^2}{\overline{z_1}(z_2 - z_3) + \overline{z_2}(z_3 - z_1) + \overline{z_3}(z_1 - z_2)} z = \frac{\begin{vmatrix}|z_1|^2 & z_1 & 1\\|z_2|^2 & z_2 & 1\\|z_3|^2 & z_3 & 1\end{vmatrix}}{\begin{vmatrix}\overline{z_1} & z_1 & 1\\\overline{z_2} & z_2 & 1\\\overline{z_3} & z_3 & 1\end{vmatrix}}\]

Also,

\[z = \frac{z_1 sin 2A + z_2 sin 2B + z_3 sin 2C}{sin 2A + sin 2B + sin 2C} \]

16.12.12. Orthocenter of a Triangle

The orthocenter \(H(z)\) of the \(\triangle ABC\) is the concurrence of altitudes of \(\triangle ABC\) and is given by

\[z = \frac{\begin{vmatrix}z_1^2 & \overline{z_1} & 1\\z_2^2 & \overline{z_2} & 1\\z_3^2 & \overline{z_3} & 1\end{vmatrix} + \begin{vmatrix}|z_1|^2 & z_1 & 1\\|z_2|^2 & z_2 & 1\\|z_3|^2 & z_3 & 1\end{vmatrix}}{\begin{vmatrix}\overline{z_1} & z_1 & 1\\\overline{z_2} & z_2 & 1\\\overline{z_3} & z_3 & 1\end{vmatrix}} \text{or} z = \frac{tanA z_1 + tanB z_2 + tanC z_3}{tanA + tanB + tanC} \text{or} z = \frac{a secA z_1 + b secB z_2 + c secC z_3}{a secA + b secB + c secC}\]

16.12.13. Euler’s Line

The centroid \(G\) of a triangle lies on the segment joining the orthocenter \(H\) and the circumcenter \(S\) of the triangle. \(G\) divides the line \(H\) and \(S\) in the ratio \(2:1.\)

16.12.14. Length of Perpendicular from a Point to a Line

Length of a perpendicular of point \(A(\omega)\) from the line \(\overline{a}z + a\overline{z} + b = 0 (a \in \mathbf{C}, b \in \mathbf{R})\) is given by

\[p = \frac{|\overline{a}\omega + a\overline{\omega} + b|}{2|a|} \]

16.12.15. Equation of a Circle

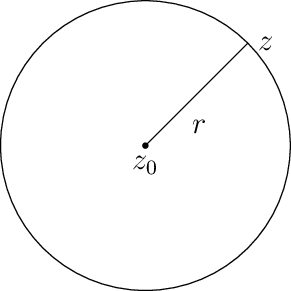
The equation of a circle with center at \(z_0\) and radius \(r\) is \(|z - z_0| = r\) or \(z = z_0 + re^{i\theta}, 0 \le \theta \le 2\pi\) (parametric form) or \(z\overline{z} - z_0\overline{z} - \overline{z_0}z + z_0\overline{z_0} - r^2 = 0\)

General equation of a circle is \(z\overline{z} - a\overline{z} + \overline{a}z + b = 0\) where \(a\) is a complex number and \(b\) is a real number such that \(\sqrt{a\overline{a} - b} \ge 0.\) Center of this circle is \(-a\) and its radius is \(a\overline{a} - b.\)

An equation of the circle one of whose diameter is the line segment joining \(z_1\) and \(z_2\) is \((z - z_1)(\overline{z} - \overline{z_2}) + (\overline{z} - \overline{z_1})(z - z_2) = 0\)

An equation of the circle passing through two points \(z_1\) and \(z_2\) is given by

\[(z - z_1)(\overline{z} - \overline{z_2}) + (\overline{z} - \overline{z_1})(z - z_2) + k \begin{vmatrix}z & \overline{z} & 1\\z_1 & \overline{z_1} & 1\\z_2 & \overline{z_2} & 1\end{vmatrix} = 0 \]

where \(k\) is a parameter.

Let us find out equation of a circle passing through three non-collinear points. Let \(A(z_1), B(z_1)\) and \(C(z_3)\) be such three points.

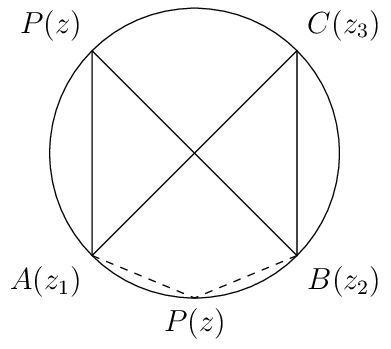
We choose \(P(z)\) any point on the circle. Two such points are shown in the figure one when it is in the same segment and other when it is in different segment.

So we have,

\[\angle ACB = \angle APB \text{ or } \angle ACB + \angle APB = \pi \]

as when \(P\) is in same segment of different.

\[arg\left(\frac{z_3 - z_2}{z_3 - z_1}\right) - arg\left(\frac{z - z_2}{z - z_1}\right) = 0 arg\left(\frac{z_3 - z_2}{z_3 - z_1}\right) + arg\left(\frac{z - z_2}{z - z_1}\right) = \pi \Rightarrow arg\left[\frac{(z_3 - z_2)(z - z_1)}{(z_3 - z_1)(z - z_2)}\right] = 0 arg\left[\frac{(z - z_1)(z_3 - z_2)}{(z - z_2)(z_3 - z_1)}\right] = \pi\]

So in both the cases the fraction must be purely real. This means

\[\frac{(z - z_1)(z_3 - z_2)}{(z - z_2)(z_3 - z_1)} = \frac{\overline{(z - z_1)(z_3 - z_2)}}{\overline{(z - z_2)(z_3 - z_1)}} \]

which can be further simplified.

From this we can also deduce the condition for four points to be concyclic. Treating \(P(z)\) as just a another point \(D(z_4)\) we can rewrite the above result as

\[\frac{(z_4 - z_1)(z_3 - z_2)}{(z_4 - z_2)(z_3 - z_1)} \]

must be purely real.

16.12.16. Finding Loci by Examination

1. \(arg(z - z_0) = \alpha\)

   If \(\alpha\) is a real number and \(z_0\) is a fixed point, then \(arg(z - z_0) = \alpha\) represents a vector starting at \(z_0\) (excluding the point \(z_0\)) and making an angle \(\alpha\) with the real \(x\)-axis.

   

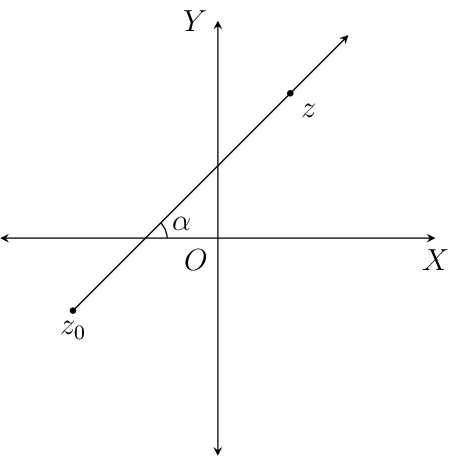
   Now suppose \(z_0\) is origin \(O\) then the above equation becomes \(arg(z) = \alpha\) which is a vector starting at origin and making an angle \(\alpha\) with the \(x\)-axis.

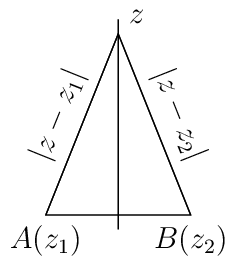
2. If \(z_1\) and \(z_2\) are two fixed points such that \(|z - z_1| = |z - z_2|\) then \(z\) represents perpendicular bisector of the segment joining \(A(z_1)\) and \(B(z_2).\) And, \(z, z_1\) and \(z_2\) will form an isosceles triangle.

   

3. If \(z_1\) and \(z_2\) are two fixed points and \(k > 0, k \ne 1\) is a real number, then

   \[\frac{|z - z_1|}{|z - z_2|} = k \]

   represents a circle.

4. \(|z - z_1| + |z - z_2| = k.\) Let \(z_1\) and \(z_2\) be two fixed points and \(k\) be a positive real number.

   1. If \(k > |z - z_2|,\) then \(|z - z_1| + |z - z_2| = k\) represents an ellipse with foci at \(A(z_1)\) and \(B(z_2)\) and length of major axis = \(k.\)

      

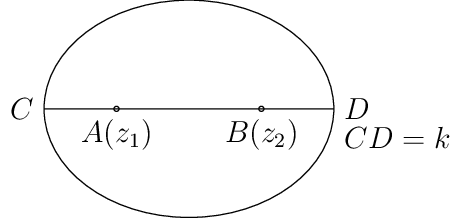
   2. If \(k = |z - z_2|\) then it represents the line segment joining \(z_1\) and \(z_2.\)

   3. If \(k < |z - z_2|\) then it does not represent any curve in Argand plane.

5. If \(|z - z_1| - |z - z_2| = k.\) Let \(z_1\) and \(z_2\) be two fixed points and \(k\) be a positive real number.

   1. If \(k \ne |z - z_2|\) then it represents a parabola with foci at \(A(z_1)\) and \(B(z_2).\)

      

   2. If \(k = |z_1 - z_2|,\) then it represents the straight line joining \(A(z_1)\) and \(B(z_2)\) but excluding the the segment \(AB.\)

      

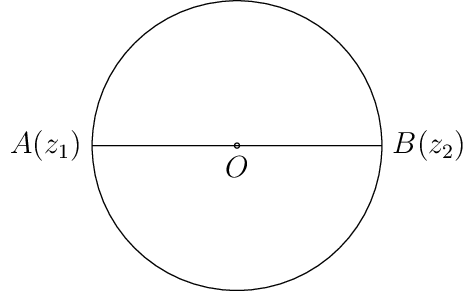
6. \(|z - z_1|^2 + |z - z_2|^2 = |z_1 - z_2|^2\). If \(z_1\) and \(z_2\) are two fixed points then it represents a circle with \(z_1\) and \(z_2\) as the end-points of one of the diameters.

   

7. \(arg\left(\frac{z - z_1}{z - z_2} = \alpha\right)\). Let \(z_1\) and \(z_1\) be any two fixed points and \(\alpha\) be a real number such that \(0 \ge \alpha \le \pi.\)

   1. If \(0 < \alpha < \pi\) and \(\alpha \ne \pi/2,\) then it represents a segment of a circle passing through \(A(z_1)\) and \(B(z_2).\)

      

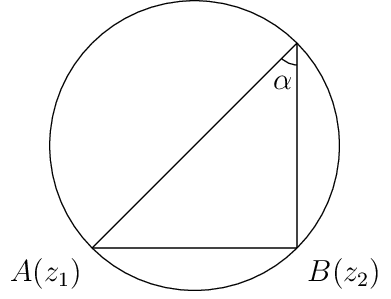
   2. If \(\alpha = \pi/2\) then it represents a circle with diameter as the line segment joining \(A(z_1)\) and \(B(z_2).\)

      

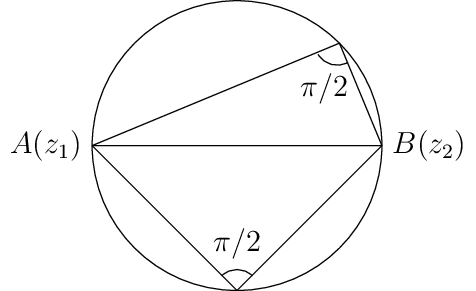
   3. If \(\alpha = \pi\) then it represents the straight line joining \(A(z_1)\) and \(B(z_2)\) but excluding the segment \(AB.\)

      

   4. If \(\alpha = 0\) then it represents the line segment joining \(A(z_1)\) and \(B(z_2).\)

      

Problems are given as a separate chapter as MathJax may end up taking long time if too much math is present on same page.