60. Permutations and Combinations#
In this chapter we will study basics of permutations and combinations. Together they are called combinatorics.
Let us say that there are three persons John, Mary and Kate. If there is one chair then in how many ways the chair can be occupied? The chair can be occupied by anyone of them. Thus, there are three ways of occupying the chair.
Let us consider another problem. Say there are two persons \(A\) and \(B\) and they have to sit in a row. One way is that \(A\) sits first and then \(B\) and the second and last obvious way is that \(B\) sits first and then \(A\). Thus, row formation in these two cases would be \(AB\) and \(BA\). Here we see that order of sitting matters.
Permutation: Permutation of objects means arrangement of objects. In permutation of objects order matter. If order of objects change then their permutation also changes.
Combination: Combination of objects means selection of objects or grouping of objects in such a way that order does not matter. Changing order does not have any effect on the final outcome as to which object is member of the group or not.
60.1. Fundamental Principle of Counting#
If a work \(A\) can be done in \(m\) ways and another work \(B\) can be done in \(n\) ways. If \(C\) is a work which can be done only if both \(A\) and \(B\) are done then total no. of ways of doing \(C\) is \(m \times n\).
60.1.1. Proof of the Multiplication Rule#
The first operation can be performed in any one of the \(m\) ways and for each of these \(m\) ways of performing the first operation there are \(n\) ways of performing the second operation. Thus, if the first operation could have been performed only in this one ways, there would have been \(1\times n = n\) ways of performing both the operations. But it is given that first operation can be performed in \(m\) ways and for each way second operation can be performed in \(n\) ways.
\(\therefore\) Total no. of ways of performing both the operations = \(n + n + n \ldots + ~\text{to}~m~\) terms \(=n\times m\)
60.2. Addition Rule#
If a work \(A\) can be done in \(m\) ways and another work \(B\) can be done in \(n\) ways and \(C\) is a work which can be done when either \(A\) or \(B\) are done then total no. of ways in which \(C\) can be done is \(m + n\) ways.
60.3. Factorial of \(n\)#
Factorial of \(n\) is denoted by \(n!\) or as the old symbol is given below:
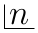
\(n!\) is given by product of first \(n\) natural numbers.
Thus, \(n! = 1.2.3.4 \ldots (n - 1).n\)
Now that we have definition of factorial we can know that for each combination of \(r\) different objects number of permutations \(=r!\)
60.4. Notations#
Number of permutations of \(n\) different objects taken \(r\) at a time is denoted by \(^nP_r\) or \(_nP_r\).
Number of combinations of \(n\) different objects taken \(r\) at a time is denoted by \(^nC_r\) or \(_nC_r\) or \(\begin{pmatrix}n\\r\\\end{pmatrix}\).
60.5. Establishing the Permutation Formula#
Let us try to find out value of \(^nP_r\). Permutation of \(n\) objects taken \(r\) at a time is equivalent to filling \(r\) different vacant spots from \(n\) different objects.
Ways to fill 1st spot = \(n\)
Ways to fill 2nd spot = \(n - 1\)
Ways to fill 3rd spot = \(n - 2\)
…
Ways to fill rth spot = \(n - r + 1\)
Total no. of ways = \(n.(n - 1).(n - 2)\ldots(n - r + 1)\)
= \(\frac{n.(n - 1).(n - 2)\ldots(n - r + 1)(n - r)\ldots 3.2.1}{(n - r)\ldots 3.2.1}\)
= \(\frac{n!}{(n - r)!}\)
Second Proof:
As given in above proof, first place can be filled in \(n\) different ways. Rest of the \(r - 1\) places can be filled from \(n - 1\) objects in \(^{n - 1}P_{r - 1}\) ways.
Hence, total no. of ways, \(^nP_r = n.^{n - 1}P_{r - 1}\)
Similarly, \(^{n - 1}P_{r - 1} = (n - 1)^{n - 2}P_{r - 2}\)
\(^{n - 2}P_{r - 2} = (n - 2).^{n - 3}P_{r - 3}\)
\(\ldots\)
\(^{n - r + 1}P_{1} = n - r + 1\)
Multiplying and cancelling common factors, we get
\(^nP_r = n.(n - 1).(n - 2)\ldots(n - r + 1) = \frac{n!}{(n - r)!}\)
60.6. \(^nP_n = n!\) and \(0!\)#
\(^nP_n = n!\) means permutation of \(n\) different objects out of \(n\). Following the formula of \(^nP_r\) we have \(^nP_n = \frac{n!}{0!}\).
However, following first proof we can say that total no. of ways = \(n!\).
Thus, \(\frac{n!}{0!} = n! \Leftrightarrow 0!= 1\)
Note that mathematically \(0!\) has no meaning.
60.7. Meaning of \(\frac{1}{(-k)!},\) where \(k\) is a positive integer#
\(^nP_r = \frac{n!}{(n - r)!}\)
Putting \(r = n + k\), we have
\(^nP_{n+k} = \frac{n!}{(-k)!}\)
But number of ways of arranging \((n + k)\) different things out of \(n\) different things \(= 0\)
\(\therefore \frac{n!}{(-k)!} = 0 \Rightarrow \frac{1}{(-k)!} = 0\)
Note: Although \((-k)!\) has no meaning by definition of factorial but if \(\frac{1}{(-k)!}\) is taken as \(0(zero)\), then the formula \(^nP_r = \frac{n!}{(n - r)!}\) will become valid even for \(r>n.\)
60.8. Permutation of Similar Objects#
To find permutation of \(n\) things taken all together when \(p\) of them are similar and are of one type, \(q\) of them are similar and are of second type, \(r\) of them are similar and are of third type and rest all are different.
Let the required no. of permutations be \(x\). Since \(p\) different things can be arranged among themselves in \(p!\) ways, therefore, if we replace \(p\) identical things by \(p\) different things then total no. of permutations will become \(p!x\). Similarly, if we replace \(q\) and \(r\) identical things by \(q\) and \(r\) different things then total no. of permutations become \(p!~q!~r!~x\).
Now all \(n\) things are different and thus no. of permutations should be \(n!\).
Thus, \(p!~q!~r!~x = n! \therefore x = \frac{n!}{p!~q!~r!}\)
60.9. Repititive Permutation#
To find number of permutations of \(n\) different things taken \(r\) at a time when each thing can be repeated \(r\) times.
Number of permutations of \(n\) different things taken \(r\) at a time when repitition is allowed = Number of ways in which \(r\) blank places can be filled by same no. of things when repitition is allowed
Now, first place can be filled by \(n\) different ways.
Second place can be filled by \(n\) different ways.
\(\ldots\)
\(r\) th place can be filled by \(n\) different ways.
Now ny multiplication rule of fundamental principle of counting number of ways in which \(r\) different places can be filled = \(n~\times~n\times\ldots r~\text{factors}\)
\(= n^r\)
60.10. Prove that \(^nP_r = r^{n - 1}P_{r - 1} + ^{n - 1}P_r\)#
\(r^{n - 1}P_{r - 1} + ^{n - 1}P_r = \frac{r(n - 1)!}{(n - r)!} + \frac{(n - 1)!}{n - r - 1}!\)
\(= \frac{r(n - 1)! + (n - r)(n - 1)!}{(n - r)!}\)
\(= \frac{(n - 1)![r + n - r]}{(n - r)!} = \frac{n(n - 1)!}{(n - r)!} = \frac{n!}{(n - r)!} = ^nP_r\)
60.11. Circular Permutation#
Let us consider about arrnging things along a circle. Let us consider that persons \(A, B, C, D\) are sitting around a round table. We can have following arrangements:
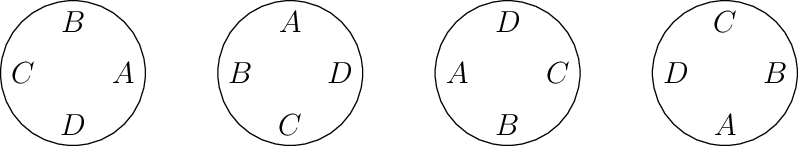
As shown four persons are sitting around a round table and four anticlockwise rotations have lead to four arrangements.
But if \(A, B, C, D\) are sitting in a row and then are shiftedd such that last occupies the place of first, then the four arrangements will be different.
Thus, if there are \(n\) things then for each circular arrangement there are \(n\) linear arrangements.
But for \(n\) different things total no. of linear arrengements are \(n!\) so the total no. of circular arrangements are \(\frac{n!}{n} = (n-1)!\)
60.12. Clockwise and Anticlockwise Arrangements#
When clockwise and anticlockwise arranegemnts are same then total no. of permutations will become half of what we computed in previous case i.e. \(\frac{(n - 1)!}{2}\)
60.13. Find the number of combinations of \(n\) different things taken \(r\) at a time(\(r\le n\))#
Number of combination of \(n\) different things taken \(r\) at a time is \(^nC_r\)
Each combination consists of \(r\) different things and these \(r\) things can be arranged among themselves in \(r!\) ways.
Thus for one combination of \(r\) things number of arrangements = \(r!\)
Therefore, number of arrangements for \(^nC_r\) = \(r!.^nC_r\)
But number of arrangements of \(n\) different things taken \(r\) at a time \(= ^nP_r\)
Thus, \(r!^nC_r = ^nP_r \therefore ^nC_r = \frac{n!}{r!(n - r)!}\)
Second Proof:
Let number of combinations of \(n\) different things taken \(r\) at a time be denoted by \(^nC_r\)
Then no. of combinations of \(n-1\) different things taken \(r - 1\) at a time be denoted by \(^{n - 1}C_{r - 1}\)
Number of combinations of \(r\) things in which a particular thing(letter) is included \(= 1.^{n - 1}C_{r - 1}\)
\(\therefore\) Total number of particular things(letters) in \(r\) combinations \(= n.^{n - 1}C_{r - 1}\)
Also, in each combination of \(r\) things number of letters \(= r\)
\(\therefore\) Total no. of letters in \(^nC_r\) combinations \(= r.^nC_r\)
Thus, we have
\(r.^nC_r = n.^{n - 1}C_{r -1} \therefore ^nC_r = \frac{n}{r}^{n - 1}C_{r - 1}\)
\(= \frac{n}{r}\frac{n - 1}{r - 1}^{n - 2}C_{r - 2}\)
\(= \frac{n}{r}.\frac{n - 1}{r - 1}. \ldots \frac{n - r + 1}{1}^{n - r}C_0\)
\(= \frac{n!}{r!~(n - r)!}\)
60.14. Properties of \(^nC_r\)#
60.14.1. Prove that \(^nC_r = ^nC_{n - r}\)#
\(^nC_r = \frac{n!}{r!~(n - r)!}\)
\(^nC_{n - r} = \frac{n!}{(n - r)!~(n - n + r)!} = \frac{n!}{(n - r)!~r!}\)
Hence proved.
60.14.2. Prove that if \(^nC_x = ^nC_y,\) then either \(x = y\) or \(x + y = n\)#
Let \(^nC_x = ^nC_y = ^nC_{n - y}\)
From first two we have \(x = y\)
From first and third \(x = n - y\) i.e. \(x + y = n\)
60.14.3. Prove that \(^nC_r + ^nC_{r - 1} = ^{n + 1}C_r\)#
\(= \frac{n!}{r!~(n - r)!} + \frac{n!}{(r - 1)!~(n - r + 1)!}\)
\(= \frac{n!}{r(r - 1)!~(n - r)!} + \frac{n!}{(r - 1)!~(n - r + 1)(n - r)!}\)
\(= \frac{n!}{(r - 1)!~(n - r)!}\left[\frac{1}{r} + \frac{1}{n - r + 1}\right]\)
\(= \frac{(n + 1)!}{r!~(n + 1 - r)!} = ^{n + 1}C_r\)
60.14.4. Prove that \(r.^nC_r = n.^{n - 1}C_{r - 1}\)#
\(= r.^nC_r = \frac{r.n.(n - 1)!}{r.(r - 1)!~(n - r)!} = n.^{n - 1}C_{r - 1}\)
60.14.5. Prove that \(\frac{^nC_r}{r + 1} = \frac{^{n + 1}C_{r + 1}}{n + 1}\)#
\(= \frac{^nC_r}{r + 1} = \frac{n!}{(r + 1)r!~(n-r)!}\)
\(= \frac{(n + 1)n!}{(n + 1)(r + 1)(n - r)!}\)
\(= \frac{1}{n + 1}.\frac{(n + 1)!}{(r + 1)!~(n - r)!} = \frac{^{n + 1}C_{r + 1}}{n + 1}\)
60.15. Restricted Combinations#
Number of combinations of \(n\) different things taken \(r\) at a time when \(p\) particular things are always selected \(= ^{n - p}C_{r - p}\)
Number of combinations of \(n\) different things taken \(r\) at a time when \(p\) particular things are excluded \(= ^{n - p}C_r\)
60.16. Selection of things#
When minimum and maximum number of things to be selected are known:
Number of selections of zero or more things out of \(n\) different things
\(= ^nC_0 + ^nC_1 + ^nC_2 + \ldots + ^nC_n = 2^n\)
Number of selections of one or more things out of \(n\) different things
\(= ^nC_1 + ^nC_2 + \ldots + ^nC_n = 2^n - 1\)
Number of selections of zero or more things out of \(n\) identical things \(= n + 1\) (since selection of \(r\) things out of \(n\) identical things can be made in \(1\) way)
Number of selections of one or more things out of \(n\) identical things \(= n\)
Number of selection of one or more things from \((p + q + r)\) things, out of which \(p\) things are identical and of one type, \(q\) things are identical and of second type, \(r\) things are identical and of third type \(= (p + 1)(q + 1)(r + 1) - 1\)
Number of selection of one of more things from \((p + q + r + n)\) things, out of which \(p\) things are identical and of one type, \(q\) things are identical and of second type, \(r\) things are identical and of third type and rest \(n\) are different
\(= (p + 1)(q + 1)(r + 1)(^nC_0 + ^nC_1 + ^nC_2 + \ldots + ^nC_n) - 1\)
\(= (p + 1)(q + 1)(r + 1)2^n - 1\)
60.17. Distribution of things among sets(groups) and persons#
Number of ways of dividing \(n\) different things in \(3\) sets containing \(x, y, z\) things, where \(x, y, z\) are distinct(here \(x + y + z = n\))
\(= ^nC_x.^{n - x}C_y.^{n - x - y}C_z = \frac{n!}{x!y!z!}\)
Number of ways of distributing \(n\) different things among \(3\) persons such that they get \(x, y, z\) things
\(= \frac{n!}{x!y!z!}3!\)
Number of ways of dividing \(n\) different things in \(5\) sets having \(a, b, c, d, e\) things(here \(a + b + c + d + e = n\))
\(= \frac{n!}{a!b!c!d!e!}\), when \(a, b, c, d, e\) are distinct
\(= \frac{n!}{a!b!c!d!e!2!3!}\), when two sets have equal no. of things and \(3\) sets have equal no. of things
\(= \frac{n!}{a!b!c!d!e!5!}\), when all the \(5\) sets have equal number of things
Number of ways of distributing above \(n\) things among \(5\) persons
\(= \frac{n!}{a!b!c!d!e!}5!\), when \(a, b, c, d, e\) are distinct
\(= \frac{n!}{a!b!c!d!e!2!3!}5!\), when \(2\) persons get equal number of things and \(3\) persons get equal number of things
\(= \frac{n!}{a!b!c!d!e!5!}5!\), when all the \(5\) persons get equal number of things.